EDICIÓN 2015
Después de pensármelo bastante voy a publicar una serie de manuales y tutoriales que hice para la comunidad de crackers en la que estuve involucrado (CracksLatinos). Los textos que publicaré intentaran sufrir la menor cantidad de modificaciones posibles.
Estos textos eran para aydar a los más novatos del grupo a coger una base y que pudiesen compartir sus conocimientos conforme vayan haciendo investigaciones.
Estos textos están datados en 3 épocas distintas, la mayoría son del 2007, antes de empezar la universidad y justo después de acabar el instituto, así que pido perdón por los errores que puedan haber en la edición original, tanto en las nociones teorícas como en la programación de las herramientas, ya que aprendí a programar (es una forma de decirlo, solo sabía escribir código, programar aprendí en la Universidad, con POO, métrica, calidad del código, patrones etc) en 1º-2º de la ESO, pero al no disponer de internet no pude mejorar hasta bastante tiempo después .
Otros textos datan del año 2009 y los últimos textos (que los los menos explicativos) datan de alrededor del 2011-2012.
Es posible que haya incoherencias en los textos puesto que no voy a publicar todos, publicaré solamente aquellos de un nivel introductorio.
Antes de cada tutorial añadiré las herramientas necesarias para poder seguir el mismo, no serán versiones actualizadas de las herramientas sino que serán las herramientas que yo usé en su día.
EDICIÓN 2007
Esta primera parte va a estar dirigida a aclarar las cosas antes de empezar, trataremos definiciones, herramientas a utilizar y mi motivación personal.
¿Qué es Cracking?
El Cracking se basa en la ingeniería inversa, que consiste en estudiar un programa para saltarse sus mediadas de protección. Mucha gente, sin saberlo, tiene pensamiento de cracker (como decía Joe Cracker), seguramente muchos de vosotros, al igual que a mi, de pequeños desmontaban los aparatos electrónicos para saber que hay dentro o como funciona el susodicho aparato.
Herramientas a utilizar y niveles de dificultad
Dentro del cracking hay diversos niveles de dificultad, desde programas que se crackean en 1 minuto hasta programas que puedes tardar meses, las protecciones que vamos a estudiar son 2, los hardcoded y los nombres/Serial.
Hardcoded: Estas medidas de seguridad ya apenas se usan por ser las mas fáciles de saltar, consiste en un código que el programa lleva dentro de sí
Nombre/Serial: Es la protección que usan la mayoría de programas, por lo general suelen ser mas difíciles que los hardcoded, aunque siempre hay excepciones. Estos sistemas no se basan en un código fijo, sino que al introducir el nombre, el programa hace una serie de operaciones con él y luego lo compara con el código que has metido.
Yo dentro de los Nombre/Serial opino que hay 3 modalidades (por decirlo de alguna manera), algunos dicen que con el fin de conseguir lo que tú quieres da igual lo que hagas (el fin justifica los medios) pero yo lo que siempre intento hacer es crackearlos de la manera mas limpia y utilizando la inteligencia, que traducido al lenguaje cracking significa hacer un keygen o en su defecto sacar el serial. (aunque no siempre se puede debido a la complejidad de algunos algoritmos), a continuación paso a explicar brevemente esas tres “modalidades” que nombro arriba.
Romper la puerta: esto quiere decir parchear el programa, también se conoce como la “Método del 74/75” (mas adelante entendereis por qué), esta es la mas fácil, solo hay que encontrar los saltos condicionales que hacen aparecer el mensaje de error de que has introducido el serial equivocado y parchearlos (Esta técnica también se puede usar en los hardcoded). Ejemplo(El código esta simplificado para que lo entendáis mejor):
CMP EAX,EBX
JNE 00401000
Esto es la estructura mas fácil que os podéis encontrar, en la primera línea lo que hace es comparar EAX y EBX (EAX y EBX son como variables, realmente se llaman registros, donde se almacenan datos del programa, hay mas “variables” como ECX, EBP, etc. eso ya se verá) y si no son iguales el programa salta a la dirección de memoria 00401000 que es el lugar donde se encuentra el mensaje de error, y justo debajo de ese salto supondremos que esta el mensaje de felicitación por haber introducido el serial correcto, así que lo que se tendría que hacer es cambiar el JNE(Saltar si no son iguales) por JE(Saltar si son iguales) de esta manera introduciendo cualquier nombre y cualquier serial registraremos el programa (a no se que acertemos el serial, ya que si acertamos el serial EAX y ECX serán iguales por lo tanto en el programa parcheado que hemos cambiado JNE por JE no nos dejaría registrarnos), y diréis ¿Qué tiene que ver esto con el 74/75? Esto se explica con la equivalencia Hexadecimal del lenguaje ASM. JE=74 y JNZ=75.
Nota: Esta estructura admite 2 soluciones más mediante el parcheo.
-
(Os recuerdo que el pc lee el programa secuencialmente de arriba hacia abajo, dicho esto explico esta forma de parcheo) Podemos cambiar el JNZ por NOP (no hacer nada) y como la zona de felicitación esta justo debajo del JNE (por que nosotros lo suponemos en este ejemplo) entonces hará la comparación, pasará por los nops sin hacer nada y finalmente llegará a la zona de de felicitación.
Aclaracion: Si os habéis dado cuenta en las imágenes de los saltos condicionales JE y JNZ a la izquierda aparecían 4 números agrupados en grupos de dos, en el de JNZ a aparecía 75 16 esto son 2 Bytes, cada par de números en hexadecimal es 1 Byte (ojo solo en el sistema hexadecimal) pues para no alterar el programa ha cambiado esos 2 bytes en 1 línea por 2 byte en 2 líneas, de ahí que el programa haya colocado 2 Nop’s en vez de 1.
Nota: encima de los saltos condicionales y de los nop’s esta la comparación.
-
Muchos dicen que poner NOP’s en un programa es ensuciarlo así que lo que prefieren hacer es poner instrucciones que dejen el programa como estaba, como por ejemplo:
Aclaración: INC = Incrementar en 1, DEC = Decrementar en 1, ya supongo que sabréis en que consiste esto, primero incremento EAX en 1 y luego lo Decremento en 1, por lo que se queda tal cual estaba al principio.
Después de esta “extensa” explicación prosigo con las demás “modalidades”
Copia de llaves: Esta táctica consiste en, mediante un “debugeo en vivo”, encontrar el serial para nuestro nombre.
Llave Maestra: Finalmente llegamos a la “modalidad” de mayor dificultad, esta quizás es la que mas se ajuste a la definición de Cracking, ya que hacer un keygen significa que comprendes el algoritmo de generación de las claves y por lo tanto has cumplido las bases de la ingeniería inversa.
Pasamos a las herramientas a utilizar
-
La herramienta esencial que utilizaremos será OLLYDBG que es un Depurador, es decir, un programa usado por los programadores para testear sus propios programas para buscar agujeros de seguridad, pero nosotros lo usaremos para hacer ingeniería inversa.
-
La segunda herramienta será un editor Hexadecimal, el que queráis como Hiew o UltraEdit.
-
Usaremos otras herramientas que ya se irán mencionando y se proporcionará el link cuando sea necesario.
Configuración del OLLYDBG
Vamos a Options>Debugging Options y a la pestaña CPU, allí seleccionamos las siguientes casillas: Show direction of jumps, Show jump path y Show grayed path if jump is not taken luego sobre donde se nos muestra el código en ASM hacemos clic con el 2º botón y elegimos Apparence > Highlighting > jumps’n’jumps.
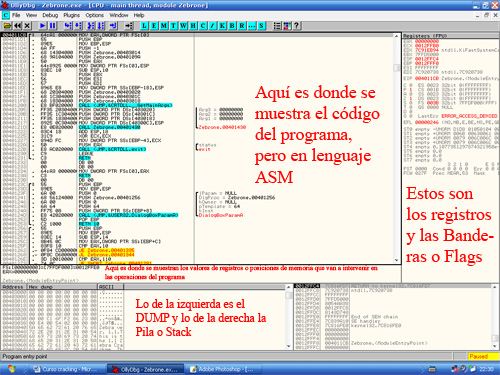
Interface del OLLYDBG
Código: Aquí es donde se muestra el código ASM del fichero que hayamos cargado, a su vez esta formado por varias parte, a la izquierda del todo se encuentran las posiciones de memoria, lo siguiente por la derecha son los Bytes (grupos de 2 en el sistema hexadecimal) lo siguiente por la derecha es la tradución a ASM de esos bytes y lo último son comentarios.
DUMP: El Dump es como si abriesemos el archivo con un editor hexadecimal, aquí se nos muestra las posiciones de memoria, los bytes y la traducción en ASCII de esos bytes.
Pila o Stack: Aquí es donde se irán guardando datos que el programa luego necesitará, la Pila o el Stack es como un mazo de cartas, cuando dejas una carta, la dejas arriba del todo y cuando sacas una la sacas de arriba del todo, las ordenes para quitar y poner valores son: PUSH, PUSHAD, POP, POPAD, PUSHA, POPA, etc… La Pila o Stack se divide en 3: de izquierda a derecha son: Posiciones de memoria, Valor colocado y Valor ASCII.
Registros y Banderas: Los registros son lugares en donde se guardan valores, estos registros son: EAX, ECX, EDX, EBX, ESP, EBP, ESI, EDI, EIP (este ultimo indica la posición de memoria que se ejecutara a continuación), Ahora veamos como se dividen los registros, imaginemos que EAX = 00112233, los últimos 4 valores se llaman AX (solo en EAX, en EBX será BX, en ECX será CX, etc…), de esta manera AX=2233 y por ultimo AX se divide en AH=22 y AL=44. Las banderas son como apoyos del programa, el programa hace una comparación y dependiendo del resultado se activa una u otra bandera, veamos las banderas:
-
C: Es el Carry flag se activa cuando se sobrepasa el maximo valor permitido, es decir, mayor a FFFFFFFF.
-
P: Bandera de Paridad se activa cuando el numero que se somete a operaciones convertido a binario tiene un número PAR de unos.
-
Z: Bandera Zero, se activa cuando ejecutamos una instrucción y el resultado es 0.
-
S: Es la Bandera de Signo y se activa cuando el numero es negativo.
-
O: Es la bandera de desbordamiento de datos (overflow).
Hay más flags, pero de momento con estos está bien.
Instrucciones básicas en ASM
INC: incrementa en 1, por ejemplo, INC EAX, esto es igual a EAX + 1.
DEC: Decrementa en 1, por ejemplo, DEC EAX, esto es igual a EAX - 1.
ADD: ADD EAX,1 es igual a INC EAX, de esta manera ADD EAX,6 es igual a EAX+6.
SUB: SUB EAX,1 es igual a DEC EAX, de esta manera SUB EAX,4 es igual a EAX-4.
NOP: No hace nada.
JE: Salto condicional que salta si los 2 registros cormprobados son iguales.
JNE: Salto condicional que salta si los 2 registros comparados no son iguales.
CMP: Compara 2 registros, ejemplo CMP EAX;EBX.
TEST: Es otro tipo de comprobación, pero se utiliza para saber si lo comprobado es 0.
PUSH: Pone el valor que hay a continuación del Push en la pila/snack, ejemplo Push 30, de esta manera colocará el valor 30 en la Pila/Stack.
POP: Quita el ultimo valor de la Pila/Sntck y lo coloca en el registro que haya a continuación, ejemplo POP EAX, esto hará que se retire el ultimo valor de la Pila/Stack y se coloque en EAX.
MOV: Mueve un valor de un lugar a otro, ejemplo MOV EAX,EBX Mueve el valor de EBX a EAX (y no al reves).
MUL: MUL es una multiplicación normal y corriente que no considera el signo, solo utiliza un operando, por que el otro operando siempre va a ser EAX, y el resultado se va a guardar EDX:EAX, esto quiere decir que EAX guarda las cifras que pueda y las que no quepan se guardan en EDX. Ejemplo: Mul EBX, multiplicará EAX * EBX y se guardará en EDX:EAX.
IMUL: IMUL es igual que la anterior con la excepción de que ahora considera el signo del número.
DIV: Como MUL pero para la división.
IDIV: Como IMUL pero para la división.
NEG: Se encarga de cambiar el signo del número.
CALL y RET: Estas instrucciones son MUY IMPORATANTES cuando hay un call lo que hace el programa es llevarte a una subrutina, es decir, el call te lleva a una zona del programa en donde se ejecutara un determinado código y acabará la ejecución cuando encuentre una instrucción RET. Cuando llega al RET el programa seguirá ejecutando la linea que hay por debajo del CALL, Puede ser que dentro de un CALL haya otro CALL a esto se le llama CALLs ANIDADOS.
Operaciones lógicas
Las operaciones lógicas se suelen hacer siempre a nivel de bits, es decir, en el sistema binario, así que veamos unos ejemplos:
OR: Se activa cuando al menos, uno de los bits es 1.
1 or 1 = 1
1 or 0 = 1
0 or 1 = 1
0 or 0 = 0
Veamos ahora una operación más compleja con OR:
10010011110010011101111000111101
00001101001110101001111001100001
10011111111110111101111001111101
AND: El resultado es 1 SOLO cuando los 2 bits son 1
1 and 1 = 1
1 and 0 = 0
0 and 1 = 0
0 and 0 = 0
Veamos ahora la operación compleja con AND:
10010011110010011101111000111101
00001101001110101001111001100001
00000001000010001001111000100001
XOR: El resultado es 1 SOLO cuando uno de los dos bits es 1 (si los 2 bits son 1 el resultado no será 1)
1 xor 1 = 0
1 xor 0 = 1
0 xor 1 = 1
0 xor 0 = 0
Operación compleja con XOR:
10010011110010011101111000111101
00001101001110101001111001100001
10011110111100110100000001011100
NOT: Esta función lo que hace es si un bit es 1 transformarlo en 0 y si es 0 ponerlo a 1:
not 1 = 0
not 0 = 1
operación compleja con NOT:
1010100110 = 0101011001
Saltos Condicionales
Antes de los saltos condicionales tiene que haber una comparación para saber si el salto se tomará o no.
CMP: Esta instrucción ya la vimos, lo que haces es comparar 2 valores, esta instrucción en realidad es una instrucción SUB que no se guarda en los registros, si los 2 valores son iguales se activará el Flag Zero (ya que el resultado es 0) y dependiendo de si es mayor o menor se activara el Flag de signo.
TEST: Esta instrucción ya la vimos, pero muy por encima, esta función en realidad es un AND que tampoco se guarda en los registros, se suele usar para comparar el mismo registro, ejemplo: TEST EBX,EBX ¿Por qué? Supongamos que EBX=1001101, la comparación entonces será
1001101
1001101
1001101
Vemos que el resultado es el mismo, ¿pero y si EAX=0000000?
0000000
0000000
0000000
Seguimos viendo que el resultado es el mismo, pero al contrario que en el ejemplo anterior (que toma un valor, pero ese valor nos da igual) aquí nos dice que vale 0, de esta manera hemos comprobado que EAX=0. Resumiendo, comparar un registro consigo mismo sirve para saber si ese registro es 0 (Esto se utiliza bastante en los algoritmos de generación de las claves)
Ahora si, vamos con los saltos condicionales
-
JE,JZ: Salta si es igual.
-
JNE,JNZ: Salta si no es igual.
-
JS: Salta si el signo es negativo.
-
JNS: Salta si el signo es positivo.
-
JMP: Salta siempre.
-
JP,JPE: Salta si hay un numero par de 1s.
-
JNP,JOP: Salta si hay un numero impar de 1s.
-
JO: Salta si se ha excedido la capacidad.
-
JNO: Salta si no se ha excedido la capacidad.
-
JB,JNAE: Salta si esta por abajo.
-
JNB,JAE: Salta si esta por encima.
-
JBE,JNA: Salta si esta por abajo o igual.
-
JNBE,JA: Salta si esta por encima o igual.
-
JL,JNGE: Salta si es menor que.
-
JNL,JGE: Salta si es mayor que.
-
JLE,JNG: Salta si es menor o igual que.
-
JNLE,JG: Salta si es mayor o igual que.
Todos los saltos condicionales se componen por la instrucción del salto seguido de la posición de memoria a la que saltará
BreakPoint
Un breakpoint es la ruputra en la ejecución de un programa, por lo general el programa se queda parado en el punto donde hayamos colocado el breakpoint hasta que demos la orden de continuar. Hay varios tipos de BreakPoint.
BreakPoint común, se suele escribir BreakPoint o BPX para abreviar
BP memory on acces, se utiliza cuando queremos que el OLLY pare al leer algo de la memoria
BP memory on write se utiliza cuando queremos que el OLLY pare al escribir algo en memoria
Hardware BreakPoint, se suelen escribir BPH y solo se pueden colocar 4 BreakPoint a la vez
Condicional BreakPoint se usan para que el OLLY pare cuando se den unas determinadas condiciones
Aún quedan algunos tipos más de BreakPoint pero ya se verán
Un BreakPoint común se pone seleccionado la línea a la que queremos ponérselo y luego a F2 o bien haciendo doble clic sobre se nos muestra las instrucciones en Hexadecimal, a la derecha de la posición de memoria y los BreakPoint se quitan haciendo clic sobre el botón B:
Eligiendo el breakpoint que quieras quitar y luego a Remove
WIN32 API
Las API’s son funciones ya creadas que lo programadores pueden utilizar en sus programas, dicho de otra manera, son funciones que vienen con el Sistema operativo y facilitan la tarea al programador, las API’s generalmente vienen en los archivos DLL del sistema, las mas importantes son Kernel32.dll y User32.dll (el 32 es por que estas API’s son para los sistemas de 32 bits y de ahí que se llamen Win32 API’s). Por ejemplo si queremos mostrar un mensaje, tenemos 2 posibilidades, o bien hacer nosotros mismo el mensaje o bien llamar a la API MessageBoxA.
Las API’s que mas se usan para coger texto son: GetDlgItemTextA y GetWindowTextA en los tutoriales ya iremos viendo mas.
Mi motivación personal
Puede sonar raro pero mi motivación personal para meterme en este mundo fue el videojuego Pokemon (concretamente los primeros pokemons, edición roja, azúl y amarilla). En estas ediciones había bastantes fallos y bastantes rumores como por ejemplo las islas fallo (error real), el valle de toguei (rumor) o el camión del SS ANNE (rumor) y es que a veces, el juego ayudaba a crear ese ambiente de rumores.
En la primera foto vemos lo que supuestamente es el valle de toguepi. En la segunda vemos esas extrañas hierbas que siempre me intrigaron, pensando que si estaban ahí es porque se podía pasar a ese lado. La tercera es como el profesor OAK pasa por esa hierba. La cuarta es missigno, al no tener ningún pokemon al que elegir y haber entrado en una pelea mi pokemon es missigno. Este último quizás es el mayor rumor, missigno, que más tarde cuando ya era un poco mayor desemsamble el código ensamblador de Pokemon Azúl.
En el juego pokemon cada pokemon tenia asignado un numero en Hexadecimal, estos números hexadecimales no podían ir desde 0 a F por que eso solo son 16 pokemon, así que lo que hicieron es ir desde 00 a FF (es decir desde 0 hasta 255), pero como todos los que hemos jugado a pokemon sabemos,en las primeras ediciones solo había 151 pokemon (Aunque hay rumores que dicen que iban a haber más pokemons) ¿Entonces que? Sobraban 105 huecos en donde debía ir algún pokemon ¿Sabéis que pokemon ocupa esos espacios? Es Missigno.
Agradecimientos
Bueno aprovecho para agradecer aquí a las personas para no tener que agradecer en cada tutorial
-
Ricardo Narvaja: Por sus magníficos conocimientos sobre cracking, su afán por enseñar y también quiero nombrar a toda la escuela de Cracker que siguen a Ricardo 😉
-
RedH@wk: por sus Crackme’s
-
Joe Cracker: Por sus crackme’s que son muy originales y aún me quedan por resolver unos cuantos.
-
Makkako: Por sus tutoriales
-
Caos Reptante: Por su magnifico manual de ASM
15 de Agosto de 2007