GZIP y SSL en servicios Web

Posted on 1 mayo, 2016 by angelluis

Al desarrollar un servicio REST es conveniente asegurar el servicio y optimizarlo, dos opciones que tenemos es utilizar comunicaciones bajo SSL y comprimir el recurso web.

Estas tareas son repetitivas y siempre que desarrollo un servicio web me toca lidiar con estos apartados y cada vez lo hago de una manera distinta así que esta vez me he decidido a documentarlo mediante un artículo para en un futuro poder tenerlo como referencia.

En este articulo voy a hablar sobre como encriptar y comprimir las comunicaciones entre un servicio REST y un cliente Android, aunque también se podrá usar una navegador, como Firefox.

El servicio REST está montado sobre una máquina Linux con PHP y desarrollado con Laravel 5.2, por otra parte en el lado del cliente se usa Android con la librería Volley para comunicaciones asincronas.

Decir que este artículo no va a tratar ni de Laravel ni de Volley, aparecerá código correspondiente a estas librerías/frameworks pero no se explicarán, así mismo la instalación y configuración inicial de apache tampoco serán explicadas.

El punto de partida es un servidor Linux con Apache y un servicio REST funcionando, por parte del cliente el punto de partida es un dispositivo Android capaz de consumir el servicio mediante Volley.

El artículo se va a dividir en 2 partes, por una parte la explicación de como hacer funcionar la compresión y por otra parte como hacer funcionar las conexiones seguras.

Comprimir la respuesta del servidor

Cuando tenemos un servicio que va a ser consumido desde un dispositivo móvil me atrevo a decir que la compresión de la respuesta es obligatoria, teniendo en cuenta que las operadoras móviles tarifican por MB consumido, comprimiendo los datos podemos reducir el tamaño en hasta 4 o 5 del tamaño original.

A diferencia de lo que mucha gente opina en internet (como por ejemplo en StackOverflow: http://stackoverflow.com/questions/21144992/android-volley-gzip-response) para hacer funcionar la compresión GZIP en volley no hace falta hacer absolutamente nada. Lo único que tenemos que configurar es nuestro servidor apache.

Primero tenemos que activar el modulo deflate que es el que nos permite realizar la compresión, para ello en la terminal ejecutamos lo siguiente

sudo a2enmod deflate

Ahora lo que tenemos que hacer es modificar el fichero /etc/apache2/apache2.conf y añadir las siguientes directivas

El commando AddOutputFilterByType DEFLATE comprimirá todo aquellos que coincida con el mime-type que le sigue, en este ejemplo comprimirá los ficheros javascript, json, xml, css...

Dependiendo del nivel de compresión que queramos podemos añadir la siguiente directiva

DeflateCompressionLevel 1-9

El valor 1 implica la mínima compresión posible y 9 la máxima. Si no especificamos comprimirá con el máximo nivel posible.

Ahora reiniciamos el servicio apache:

sudo service apache2 restart

Para hacer las pruebas me he creado un recurso simple en laravel

Donde lo que se imprime es un texto bastante grande generado mediante un Lorem ipsum generator (http://es.lipsum.com/).

Si accedemos al recurso en firefox y presionamos Ctrl + Shift + C y vamos a la pestaña “Network”

veremos lo siguiente (Si no aparece nada, una vez se esté posicionado en la pestaña network volver a cargar el recurso)

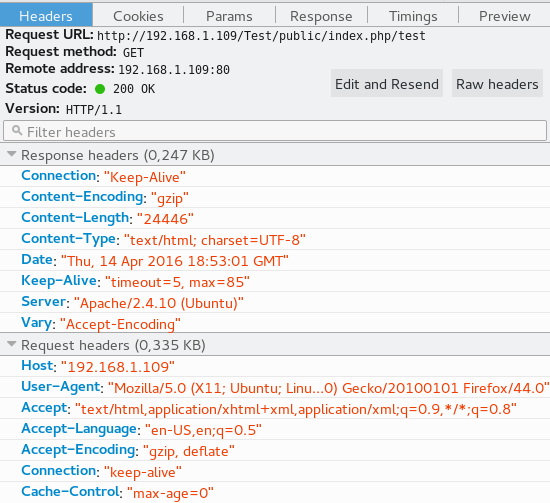
Podemos ver como el tamaño es de 89KB pero lo que se ha transimitido es 23.87KB, unas 4 veces menos, una ahorro a tener muy en cuenta. Si pulsamos sobre esta petición podremos ver lo siguiente:

Podemos ver como en las cabeceras de la petición (Request headers) podemos ver la cabecera:

Accept-Encoding: “gzip, deflate”

y en las cabeceras de la respuesta (Response headers) podemos ver la cabecera:

Content-Encoding: “gzip”

Esas 2 cabecerás es lo único necesario para que funcione la compresión GZIP. ¿Pero esto funciona en Volley? Vamos a comprobarlo, para ello vamos a usar wireshark y esnifar las comunicaciones.

En mi caso tengo mi router (192.168.1.101), mi servidor linux (192.168.1.109) y mi Android, del cual no se su ip ni me interesa. Tras una petición de Android el flujo de comunicación será el siguiente:

1 – Android manda la petición a mi router

2 – Mi router envia la petición al servidor

3 – El procesa la petición y genera la respuesta, y la manda al router

4 – Finalmente el router reenvia la petición a mi Android.

Abrimos ahora wireshark y empezamos a capturar tráfico, ahora nos dirijimos a la aplicación Android y hacemos la petición al servidor, cuando hayamos mandado la petición y hayamos recibido la respuesta pausamos wireshark.

Seguramente aunque lo hayamos estado capturando tráfico solamente durante unos segundos tendremos miles de entradas en wireshark. Para aclararnos un poco tenemos que usar la busqueda mediante filtros, para encontrar la petición basta con usar el siguiente comando:

http.request.uri matches "example"

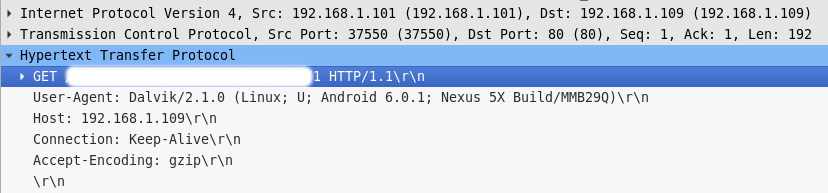
En example debemos poner alguna parte que sepamos de la url de nuestro recurso y así podremos localizar nuestra petición y ver lo siguiente

Esta vez he eliminado la URL de la petición ya que uso un servicio privado. Pero podemos ver como volley ha añadido la cabecera

Accept-Encoding: gzip

Ahora para localizar la respuesta del servidor podemos usar el siguiente filtro

ip.src == 192.168.1.109 && ip.dst == 192.168.1.101 && http

Podemos ver como el servidor contesta con la cabecera

Content-Encoding: gzip

Además Wireshark nos dice en la penultima linea que el contenido está codificado con GZIP

Por tanto, resumiendo, volley añade automáticamente la cabecera necesaria para comprimir los datos (esto lo hace mediante el uso de la clase HttpUrlConnection) por contra para que el servidor acepte compresión por GZIP hay que seguir los pasos explicados anteriormnete

IMPORTANTE: Bajo ningún concepto añadir manualmente la cabecera Accept-Encoding: gzip en el método getHeaders de la Request de Volley ya que si se añade la cabecerá manualmente habrá que hacer la descompresión de los datos en GZIP manualmente mediante GZIPInputStream. Tamibén es impostante saber que la clase HttpUrlConnection unicamente está disponible a partir de la API 9 de Android en versiones anteriores usa HttpClient y por tanto la descompresión habrá que hacerla manualmente.

Establecer comunicaciones seguras

En esta parte hay una mayor carga teórica, la cual no voy a explicar, entiendo que si alguien encuentra esto es porque tiene nociones de certificados, autoridades de certificación, cadenas de confianza y claves privadas.

Para empezar debemos generar nuestro certificado y nuestra clave privada, para ello podemos utilizar openssl en linux,

openssl req -x509 -newkey rsa:2048 -keyout key.pem -out cert.crt -days 1000

con openssl hacemos una petición de certificado x509 generando con ello una nueva clave privada RSA de 2048 bits llamada key.pem, el certificado generado será cert.crt y tendrá una validez de 1000 días.

A continuación debemos guardar estos dos ficheros generados en un lugar seguro, por ejemplo /etc/apache2/ssl

Ahora tenemos que configurar un host virtual con ssl, por lo general apache viene con uno por defecto, para activarlo debemos ejecutar el siguiente comando:

sudo a2ensite default-ssl.conf

Las 2 primeras líneas de este fichero son

<IfModule mod_ssl.c>

<VirtualHost _default_:443>

Si queremos podemos cambiar el puerto que por defecto es el 443. Tenemos que asegurarnos de que está presente la siguiente directiva

SSLEngine on

y especificar nuestro certificado y clave privada

SSLCertificateFile /etc/apache2/ssl/cert.crt
SSLCertificateKeyFile /etc/apache2/ssl/key.pem

Por último reiniciamos apache mediante

sudo service apache2 restart

Si ahora accedemos al recurso mediante un navegador como firefox (y mediante el protocolo HTTPS y no HTTP) se mostrará lo siguiente

Si vamos a Advanced y le damos a Add Exception… y luego a Confirm Security Exception ya podremos acceder al recurso. Ahora falta modificar la aplicación Android para que sea capaz de comunicar mediante ssl con el servicio web.

Ahora si abrimos las herramientas de desarrollador de firefox con Ctrl + Shift + C

Vemos como ha aparecido un candado a la izquierda del dominio y además aparece información de seguridad.

Lo primero que debemos hacer es generar un keystore para almacenar nuestro certificado y poder usarlo en Android, para ello nos bajamos de aquí el fichero bcprov-ext-jdk15on-1.46.jar y ejecutamos la siguiente línea en la terminal de Linux

sudo keytool -importcert -v -trustcacerts -file cert.crt -alias IntermediateCA -keystore "./keystore.bks" -provider org.bouncycastle.jce.provider.BouncyCastleProvider -providerpath bcprov-ext-jdk15on-1.46.jar -storetype BKS -storepass "PASSWORD"

Debemos ejecutarlo desde el directorio donde tengamos el fichero bcprov-ext-jdk15on-1.46.jar y el certificado.

Con esto se nos habrá creado un fichero con extensión bks que debemos importar en la carpeta RAW de Android.

En Android lo que debemos hacer ahora es cambiar las rutas y cambiar http por https. Por ejemplo yo siempre tengo las rutas en constantes de la siguiente forma

El tema de las interrogaciones es por el hecho de que siempre que uso URL's me genero un sistema de bindings de parámetros.

A continuación debemos crear un nuevo stack para Volley, en mi caso a dicha clase le he llamado HurlSslStack que extiende de HurlStack. En esta clase lo que debemos hacer es crear el contexto SSL, para ello el constructor de clase recibe un stream del keystore que hemos creado más arriba. En esta clase debemos implementar el método createConnection que será el encargado de crear la conexión, crear el contexto SSL y verificar el host, para verificar el host debemos verificar que el campo "Issue to" o "Emitido a" cuando hemos creado el certificado coincide.

Intersecciones entre rayos, esferas y triángulos

Posted on 20 enero, 2016 by angelluis

La semana pasada estuve teniendo bastantes problemas con la intersección entre rayos y esferas y entre rayos y triángulos. Para no reinventar la rueda opté por usar implementaciones ya existentes, concretamente usé implementaciones de los libros Real-Time Rendering y Real-Time Collision y en principio parecían funcionar, el problema fue cuando añadí transformaciones a los objetos 3D.

Cuando implementé las transformaciones, los objetos no se renderizaban correctamente y estuve bastante tiempo averiguando que es lo que pasaba, pensé que al coger implementaciones de libros tan reconocidos éste no sería el problema, hasta que descartando problemas solo me quedó que los algoritmos de intersección estuviesen mal implementados.

Lo que hice al principio fue buscar por internet otra implementación para no perder mucho el tiempo en implementar yo mismo un algoritmo relativamente sencillo, mi sorpresa fue que tampoco conseguí hacer funcionar las transformaciones en RTal con estos algoritmos. Había probado ya 3 algoritmos distintos y ninguno funcionaba correctamente con las transformaciones, así que finalmente hice lo que debía haber hecho desde un principio, implementarlos yo mismo.

Este artículo va a tratar de como implementar intersecciones entre rayos y esferas y entre rayos y triángulos, intentaré que sea lo más claro posible incluso para aquellas personas que no están muy familiarizadas con la geometría y las matemáticas.

Voy a empezar explicando que es un "rayo" que quizá es un concepto extraño para aquel que no esté familiarizado con el tema.

Un rayo es un concepto geométrico que empieza en un punto y se extiende de manera infinita en una dirección y en un único sentido. Un rayo está muy relacionado con el concepto de linea y de segmento. Una línea se extiende de manera infinita en una dirección y en ambos sentidos, un segmento es un fragmento de recta que une 2 puntos del espacio.

Las definición matemática de rayo, línea y segmento respectivamente es

$R(t) = \textbf{o} + t*\hat{d}$

$L(t) = (1-t)\textbf{a} + t*\textbf{b}$

$S(t) = \textbf{a} + t* (\textbf{b}-\textbf{a})$

En este caso nos interesa solamente el concepto de rayo que es el que se usa en los sistemas de Ray Tracing, el origen del rayo por lo general es la camara o un punto de intersección de la escena y la dirección es la coordenada del pixel que se está calculando, en un futuro artículo hablaré de esto.

Nota: La notación $\textbf{a}$ significa que estamos hablando de un vector y la notación $\hat{a}$ significa que estamos hablando de un vector unitario que se define de la siguiente forma

$\hat{v} = \hat{(x,y,z)} = \frac{\textbf{v}}{||\textbf{v}||}$

donde

$||\textbf{v}|| = \sqrt[2]{x^2 + y^2 + z^2}$

Intersección entre esferas y rayos

Empecemos con las intersecciones entre rayos y esferas.

La definición matemática de una esfera es la siguiente

$(\textbf{p}-\textbf{c})\cdot(\textbf{p}-\textbf{c}) - r^2 = 0$

Donde $\textbf{c}$ es el centro de la esfera y $\textbf{p}$ es un punto cualquiera de su superficie y $r$ es el radio de la esfera, recordemos que el producto punto de dos vectores o dot product es un escalar y se define como

$(a,b,c)\cdot(x,y,z) = a*x + b*y + c*z$

Para encontrar intersecciones entre rayos y esferas basta con definir $\textbf{p}$ de la siguiente forma $\textbf{p} = \textbf{o} + t*\hat{d}$ de esta manera sustituyendo en la ecuación de la esfera $\textbf{p}$ por la ecuación del rayo obtenemos

$(\textbf{o} + t\hat{d} - \textbf{c}) \cdot (\textbf{o} + t\hat{d} - \textbf{c}) - r^2 = 0$

Esta ecuación es una ecuación cuadrática que si simplificamos obtenemos

$t^2(\hat{d}\cdot \hat{d}) + 2t(\hat{d} \cdot (\textbf{o} - \textbf{c})) + (\textbf{o} - \textbf{c}) \cdot (\textbf{o} - \textbf{c}) - r^2 = 0$

Al resorver esta ecuación hay que tener encuenta que las ecuaciones cuadráticas tienen como máximo 2 soluciones (raices) y estas solucciones tienen sentido geométrico.

Si no hay ninguna solución entonces no se ha producido ninguna intersección.
Si hay 2 soluciones significa que el rayo ha entrado en la esfera en un punto del espacio y ha salido en otro punto distinto, en este caso nos interesa el solucion que represente un punto más cercano al origen del rayo.
- Si hay 2 soluciones positivas nos quedamos con la produzca el punto más cercano al origen del rayo.
- Si hay una solución positiva y otra negativa nos quedamos con la solución positiva.
- Si las 2 soluciones son negativas no se produce intersección.
Si solo hay una ecuación significa que el rayo pasa tangente a la esfera.

Una implementación sencilla de las ecuaciones y el proceso explicado sería la siguiente (las 2 primeras líneas del método hit sirven para transformar el rayo en el sistema local de coordenadas de la esfera y así poder realizar de forma sencilla la intersección con esferas transformadas)

Intersección entre rayos y triángulos

Un triángulo está definido por 3 puntos en el espacio llamados vértices (vertex), la unión de estos vértices forman lo que se conoce como aristas (edge) y por lo general un triángulo representa una cara (face).

La intersección entre rayos y triángulos es un poco más compleja pero relativamente sencilla, para saber si un rayo produce una intersección con un triángulo debemos llevar a cabo 2 comprobaciones, la primera es si el rayo intersecta con el plano (infinito) que contiene al triángulo y la segunda comprobar que el punto de intersección (generado por el rayo y el plano) está dentro del triángulo. Así que vamos a dividir esta explicación en 2 partes

Intersección Rayo-Plano

Un plano se define como

$ax + by + cz = d$

También se puede definir de forma vectorial de la siguiente forma

$\hat{n} \cdot (\textbf{x} - \textbf{p}) = 0$

$\hat{n}$ es el vector normal y representa la dirección de la superficie, el producto punto puede representar el coseno del angulo formado por dos vectores, en este caso tiene sentido, si cogemos el vector normal (dirección de la superficie del plano) y un vector del plano, tenemos que el ángulo entre ambos vectores forma $90^\circ$ y $cos(90) = 0$ podemos desarrollar un poco más la fórmula del plano y llegar a

$\hat{n} \cdot \textbf{x} = \hat{n} \cdot \textbf{p}$

Si definimos $\hat{n} \cdot p$ como la distancia desde el origen de coordenadas al plano ( $d$ ) tenemos la siguiente ecuación

$\hat{n} \cdot \textbf{x} = d$

Ya sabemos todo lo que tenemos que saber sobre un plano, ahora para encontrar la intersección entre un rayo y el plano basta con susituir la ecuación del rayo ( $R(t) = \textbf{o} + t*\hat{d}$ ) en la variable $\textbf{x}$ del plano, de esta manera tenemos

$\hat{n} \cdot R(t) = d \longrightarrow \hat{n} \cdot (\textbf{o} + t*\hat{d}) = d \longrightarrow \hat{n} \cdot \textbf{o} + \hat{n}*t \cdot \hat{d} = d$

No confundir $d$ que es la distancia desde el origen de coordenadas al plano con $\hat{d}$ que es la dirección del rayo.

Para resolver esta ecuación tenemos que calcular antes una serie de variables que todavía no conocemos como $\hat{n}$ y $d$ . El vector normal de un plano que contiene un triángulo es el vector normal del triángulo y el vector normal de un triángulo es

$\hat{n} = \frac{(\textbf{b}-\textbf{a}) \times (\textbf{c}-\textbf{a})}{|(\textbf{b}-\textbf{a}) \times (\textbf{c}-\textbf{a})|}$

Donde $\times$ es el producto vectorial y se puede definir de la siguiente forma

$(x,y,z) \times (a,b,c) = \begin{vmatrix} \textbf{i} & \textbf{j} & \textbf{k} \\ a & b & c \\ x & y & z \end{vmatrix} = \textbf{i} \begin{vmatrix} b & c \\ y & z \end{vmatrix} - \textbf{j} \begin{vmatrix} a & c \\ x & z \end{vmatrix} + \textbf{k} \begin{vmatrix} a & b \\ x & y \end{vmatrix}$

Formando $\textbf{i}, \: \textbf{j} \: y \: \textbf{k}$ una base de coordenadas ortonormal y en muchos casos $\textbf{i}=(1,0,0), \: \textbf{j}=(0,1,0) \: y \: \textbf{k}=(0,0,1)$

Teniendo calculado $\hat{n}$ ya solo nos queda calcular la distancia desde el origen $d$ , para ello basta con sustituir todos los datos que tenemos en la ecuación del plano y como punto del plano podemos elegir cualquiera de los vertices del triángulo

$\hat{n} \cdot \textbf{a} = d$

Ahora podemos calcular $t$ para averiguar en que punto el rayo intersecta con el plano

$t = \frac{d-\hat{n} \cdot \textbf{o}}{\hat{n}\cdot \hat{d}}$

¡Ojo! Si $\hat{n}\cdot \hat{d} = 0$ significa que el rayo es paralelo al plano y esto habrá que tenerlo en cuenta a la hora de realizar la implementación.

Ahora podemos calcular el punto donde intersecta el rayo con el plano de la siguiente forma

$\textbf{q} = \textbf{o} + t*\hat{d}$

Comprobando si el punto de intersección está dentro del triángulo

Calculado el punto de intersección (si es que lo hay) ahora tenemos que ver si dicho punto está dentro de todos los bordes del triangulo, si lo está concluiremos que el rayo ha intersectado con el triángulo y procederemos a calcular las coordenadas de intersección.

Para comprobar en lado de un borde se encuentra un determinado punto podemos usar la siguiente fórmula

$[(\textbf{b} - \textbf{a}) \times (\textbf{q} - \textbf{a})] \cdot \hat{n} \geqslant 0$

Deberemos hacer esta comprobación para los 3 bordes

$[(\textbf{b} - \textbf{a}) \times (\textbf{q} - \textbf{a})] \cdot \hat{n} \geqslant 0$

$[(\textbf{c} - \textbf{b}) \times (\textbf{q} - \textbf{b})] \cdot \hat{n} \geqslant 0$

$[(\textbf{a} - \textbf{c}) \times (\textbf{q} - \textbf{c})] \cdot \hat{n} \geqslant 0$

Por último resta saber las coordenadas de la intersección, para ello deberemos usar las coordenadas baricéntricas $\alpha, \: \beta \: y \: \gamma (0 \leqslant \alpha \: \beta \: \gamma \leqslant 1)$

Dichas coordenadas baricéntricas se pueden calcular en relación al area del triángulo

$\alpha = \frac{Area(QBC)}{Area(ABC)} \: \beta = \frac{Area(AQC)}{Area(ABC)} \: \gamma = \frac{Area(ABQ)}{Area(ABC)}$

El producto vectorial tiene un sentido geométrico bastante interesante y es que la magnitud del mismo representa el area formada por los vectores involucrados en el producto vectorial. Teniendo el vector normal $\hat{n}$ podemos expresar la magnitud del producto vectorial de la siguiente forma

$|(\textbf{c}-\textbf{b}) \times (\textbf{q}-\textbf{b})| = [(\textbf{c}-\textbf{b}) \times (\textbf{q}-\textbf{b})] \cdot \hat{n}$

De esta manera tenemos

$\alpha = \frac{[(\textbf{c} - \textbf{b}) \times (\textbf{q}-\textbf{b})] \cdot \hat{n}}{[(\textbf{b} - \textbf{a}) \times (\textbf{c}-\textbf{a})] \cdot \hat{n}} \: \beta = \frac{[(\textbf{a} - \textbf{c}) \times (\textbf{q}-\textbf{c})] \cdot \hat{n}}{[(\textbf{b} - \textbf{a}) \times (\textbf{c}-\textbf{a})] \cdot \hat{n}} \: \gamma = \frac{[(\textbf{b} - \textbf{a}) \times (\textbf{q}-\textbf{a})] \cdot \hat{n}}{[(\textbf{b} - \textbf{a}) \times (\textbf{c}-\textbf{a})] \cdot \hat{n}}$

Con esto hemos hallado las coordenadas baricéntricas, ahora nos falta hallar el punto de intersección del rayo con el triángulo, para ello basta multiplicar las coordenadas baricéntricas con sus respectivos vértices:

$p_{interseccion} = a*\alpha + b*\beta + c*\gamma$

Una implementación de este algoritmo seria la siguiente (de nuevo, las dos primeras líneas del método hit son para transformar el rayo al sistema de coordenadas locales del triángulo, para optimizar se podría hacer la comprobación de la intersección en el sistema de coordenadas global en vez del local)

A continuación una serie de imagenes generadas con RTal que implementa estos algoritmos (https://github.com/RdlP/RTal)

Demo de ALPhysics.js

Posted on 25 octubre, 2015 by angelluis

Como anuncié en la anterior entrada estoy desarrollando una librería de simulación física en tiempo real, actualmente está en una versión muy temprana y solo admite fuerzas gravitatorias.

He decidido dejar solamente un método de integración, el método de euler, hasta que se requieran métodos más precisos.

Aquí dejo la demostración, montada sobre un escenario 2D

http://angelluispg.es/AL3D/physics/